Advertisements
Advertisements
प्रश्न
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
उत्तर

Given: Two tangents PQ and PR are drawn from an external points P to a circle with centre O.
To prove: Centre of a circle touching two intersecting lines lies on the angle bisector of angle formed by tangents.
Construction: Join OR and OQ.
In ∆POR and ∆POQ,
∠PRO = ∠PQO = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
OR = OQ ...[Radii of same circle]
Since, OP is common
∴ ∆PRO ≅ ∆PQO ...[RHS]
Hence, ∠RPO = ∠QPO ...[By CPCT]
Thus, O lies on angle bisector of PR and PQ.
Hence proved.
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

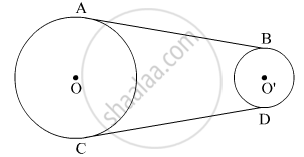
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
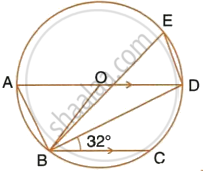
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of tangents drawn from an external point to the circle ______
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

