Advertisements
Advertisements
प्रश्न
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

उत्तर
In ΔADB,
∠ADB = 90° (Angle in semi-circle) ...(i)
Now, by using angle sum properly in ΔABD, we have
∠ABD + ∠ADB + ∠DAB = 180°
⇒ ∠ABD + 90° + 55° = 180° ...[From equation (i) and given ∠DAB = 55°]
⇒ ∠ABD = 180° – 145°
⇒ ∠ABD = 35° ...(ii)
Now, ∠ABD = 90° ...(Angle between tangent and radius)
or, ∠ABD + ∠DBC = 90°
or, ∠DBC = 90° – ∠ABD
or, ∠DBC = 90° – 35° ...[From equation (ii)]
or, ∠DBC = 55°
Alternate Method: Since, the angle between chord and tangent is equal to the angle subtended by the same chord in alternate segment of the circle, Hence, ∠BDC = ∠BAD = 55°.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
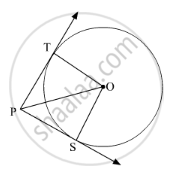
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
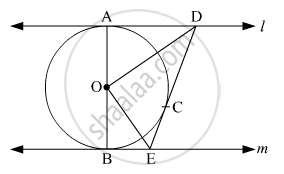
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
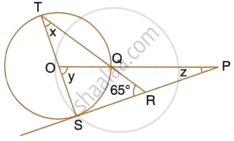
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
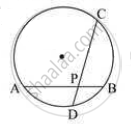
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
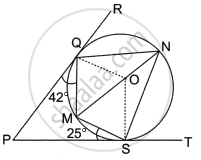
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
