Advertisements
Advertisements
प्रश्न
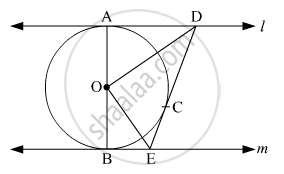
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
उत्तर
Given: l and m at are two parallel tangents to the circle with centre O touching the circle at A and B respectively. DE is a tangent at the point C, which intersects l at D and m at E.
To prove: ∠ DOE = 90°
Construction: Join OC.
Proof:
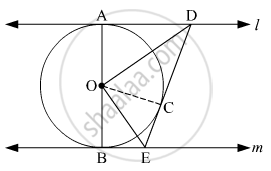
In ΔODA and ΔODC,
OA = OC (Radii of the same circle)
AD = DC (Length of tangents drawn from an external point to a circle are equal)
DO = OD (Common side)
ΔODA ≅ ΔODC (SSS congruence criterion)
∴ ∠DOA = ∠COD … (1) (C.P.C.T)
Similarly, ΔOEB ≅ ΔOEC
∠EOB = ∠COE … (2)
AOB is a diameter of the circle. Hence, it is a straight line.
∴ ∠DOA + ∠COD + ∠COE + ∠EOB = 180º
From (1) and (2), we have
2∠COD + 2 ∠COE = 180º
⇒ ∠COD + ∠COE = 90º
⇒ ∠DOE = 90°
Hence, proved.
APPEARS IN
संबंधित प्रश्न
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°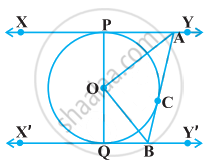
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

