Advertisements
Advertisements
प्रश्न
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
उत्तर
Two tangents PA and PB are drawn to a circle with centre O from an external point P

Perimeter of ΔPCD = PC + CD + PD
= PC + CE + ED + PD
= PC + CA + DB + PD
= PA + PB
= 2PA
= 2(10)
= 20 cm ...[∵ CE = CA, DE = DB, PA = PB tangents from internal point to a circle are equal]
संबंधित प्रश्न
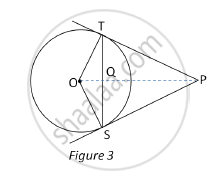
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of the tangent from an external point P on a circle with centre O is ______
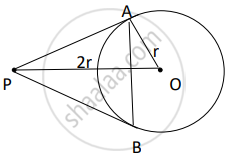
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

