Advertisements
Advertisements
प्रश्न
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
उत्तर १
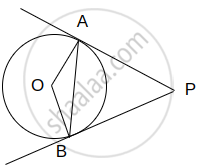
Given: PA and PB are the tangent drawn from a point P to a circle with centre O. Also, the line segments OA and OB are drawn.

To Prove: ∠APB + ∠AOB = 180°
Proof: We know that the tangent to a circle is perpendicular to the radius through the point of contact.
Now, in right ΔOAP and right ΔOBP, we have PA = PB ...[Tangents to circle from an external point]
OA = OB ...[Radii of the same circle]
OP = OP ....[Common]
ΔOAP ≅ ΔOBP ....[by SSS congrurncy]
∠OPA = ∠OPB
and ∠AOP = ∠BOP
⇒ ∠APB = 2∠OPA and ∠AOB = 2∠AOP
In right ΔOAP
⇒ ∠AOP + ∠OPA + ∠PAO = 180°
⇒ ∠AOP = 180° − 90° − ∠OPA
⇒ ∠AOP = 90° − ∠OPA
⇒ 2∠AOP = 180° − 2∠OPA
⇒ ∠AOB = 180° − ∠APB
⇒ ∠AOB + ∠APB = 180°
उत्तर २

Let us consider a circle centered at point O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.
It can be observed that
OA (radius) ⊥ PA (tangent)
Therefore, ∠OAP = 90°
Similarly, OB (radius) ⊥ PB (tangent)
∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP + ∠APB + ∠PBO + ∠BOA = 360º
90º + ∠APB + 90º + ∠BOA = 360º
∠APB + ∠BOA = 180º
Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
Prove that a parallelogram circumscribing a circle is a rhombus.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
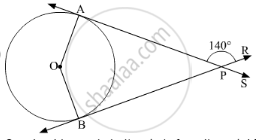
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
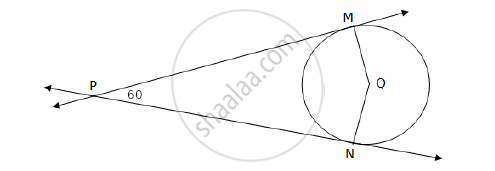
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
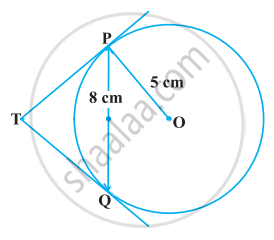
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.