Advertisements
Advertisements
प्रश्न
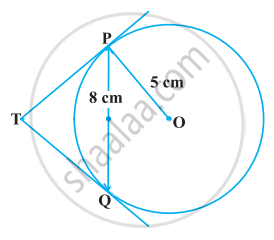
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
उत्तर
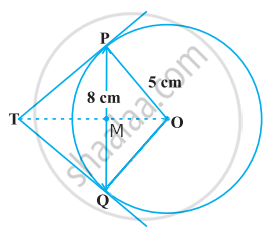
Given radius, OP = OQ = 5 cm
Length of the chord, PQ = 8 cm
OT ⊥ PQ,
∴ PM = MQ = 4 cm ......[Perpendicular draw from the centre of the circle to a chord bisect the chord]
In right ΔOPM,
OP2 = PM2 + OM2
⇒ 52 = 42 + OM2
⇒ OM2 = 25 – 16 = 9
Hence OM = 3 cm
In right ΔPTM,
PT2 = TM2 + PM2 ......(1)
∠OPT = 90° ......[Radius is perpendicular to the tangent at the point of contact]
In right ΔOPT,
OT2 = PT2 + OP2 ......(2)
From equations (1) and (2), we get
OT2 = (TM2 + PM2) + OP2
⇒ (TM + OM)2 = (TM2 + PM2) + OP2
⇒ TM2 + OM2 + 2 × TM × OM = TM2 + PM2 + QP2
⇒ OM2 + 2 × TM × OM = PM2 + OP2
⇒ 9 + 6TM = 16 + 25
⇒ 6TM = 32
⇒ TM = `32/6 = 16/3`
Equation(1) becomes,
PT2 = TM2 + PM2
= `(16/3)^2 + 4^2`
= `(256/9) + 16`
= `(256 + 144)/9`
= `(400/9)`
= `(20/3)^2`
PT = `20/3`
This gives `("TP")/("PO") = ("RP")/("RO")`, i.e., `("TP")/5 = 4/3` or TP = `20/3` cm.
संबंधित प्रश्न
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
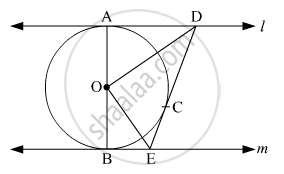
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
The length of the tangent from an external point P on a circle with centre O is ______
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
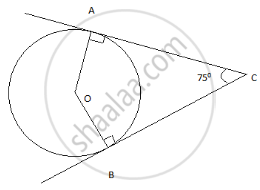
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
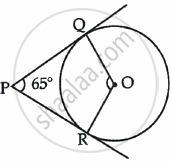
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.