Advertisements
Advertisements
प्रश्न
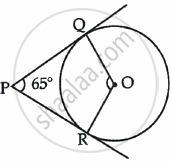
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
विकल्प
65°
125°
115°
90°
उत्तर
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is 115°.

Explanation:
∠QPR + ∠QOR = 180°
∴ ∠QOR = 180° – ∠QPR
= 180° – 65°
= 115°
संबंधित प्रश्न
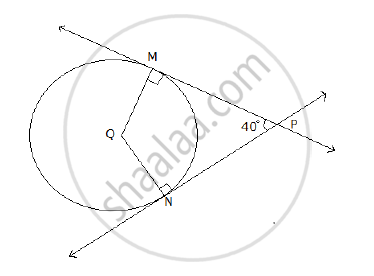
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
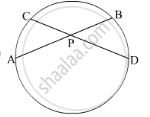
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
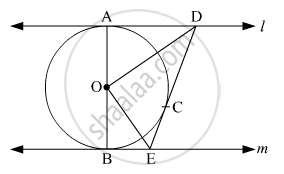
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
The angle between two tangents to a circle may be 0°.
The length of tangent from an external point P on a circle with centre O is always less than OP.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
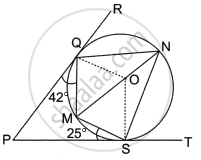
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
