Advertisements
Advertisements
प्रश्न
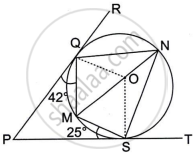
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
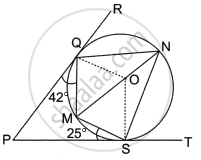
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
उत्तर
a. PR and PT are tangents to the circle with centre O.
Then, ∠OQP = 90°
As, radius is ⊥ to the tangent
Then, ∠OQM = ∠OQP – ∠MQP
= 90° – 42°
= 48°
b. ∠PQM = ∠QNM = 42° ...(By alternate segment theorem)
∠PSM = ∠SNM = 25°
Then ∠QNS = ∠QNM + ∠SNM
= 42° + 25°
= 67°
c. ∠QOS = 2∠QNS ...(since, angle subtended by the arc at the centre is twice the angle subtended by the arc at any other point of the circles.)
= 2 × 67°
= 134°
d. QNSN is a cyclic quadritateral
∠QNS + ∠QMS = 180°
∠QMS = 180° – 67° = 113°
APPEARS IN
संबंधित प्रश्न
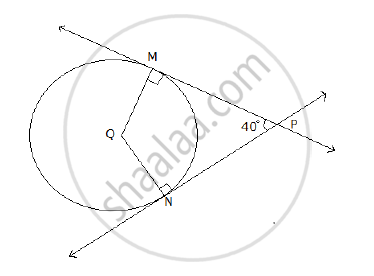
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.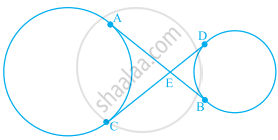
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
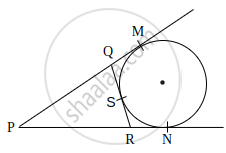
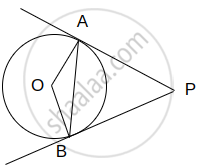
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.