Advertisements
Advertisements
Question
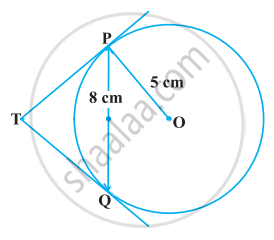
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Solution
Given radius, OP = OQ = 5 cm
Length of the chord, PQ = 8 cm
OT ⊥ PQ,
∴ PM = MQ = 4 cm ......[Perpendicular draw from the centre of the circle to a chord bisect the chord]
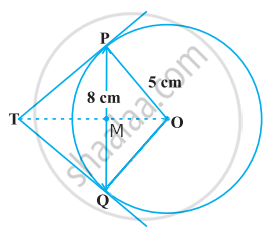
In right ΔOPM,
OP2 = PM2 + OM2
⇒ 52 = 42 + OM2
⇒ OM2 = 25 – 16 = 9
Hence OM = 3 cm
In right ΔPTM,
PT2 = TM2 + PM2 ......(1)
∠OPT = 90° ......[Radius is perpendicular to the tangent at the point of contact]
In right ΔOPT,
OT2 = PT2 + OP2 ......(2)
From equations (1) and (2), we get
OT2 = (TM2 + PM2) + OP2
⇒ (TM + OM)2 = (TM2 + PM2) + OP2
⇒ TM2 + OM2 + 2 × TM × OM = TM2 + PM2 + QP2
⇒ OM2 + 2 × TM × OM = PM2 + OP2
⇒ 9 + 6TM = 16 + 25
⇒ 6TM = 32
⇒ TM = `32/6 = 16/3`
Equation(1) becomes,
PT2 = TM2 + PM2
= `(16/3)^2 + 4^2`
= `(256/9) + 16`
= `(256 + 144)/9`
= `(400/9)`
= `(20/3)^2`
PT = `20/3`
This gives `("TP")/("PO") = ("RP")/("RO")`, i.e., `("TP")/5 = 4/3` or TP = `20/3` cm.
RELATED QUESTIONS
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
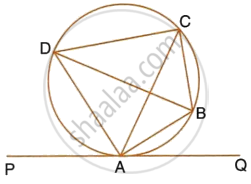
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
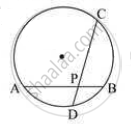
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
The angle between two tangents to a circle may be 0°.
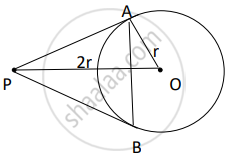
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.