Advertisements
Advertisements
Question
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.
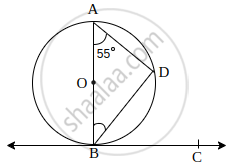
Solution
In ΔADB,
∠ADB = 90° (Angle in semi-circle) ...(i)
Now, by using angle sum properly in ΔABD, we have
∠ABD + ∠ADB + ∠DAB = 180°
⇒ ∠ABD + 90° + 55° = 180° ...[From equation (i) and given ∠DAB = 55°]
⇒ ∠ABD = 180° – 145°
⇒ ∠ABD = 35° ...(ii)
Now, ∠ABD = 90° ...(Angle between tangent and radius)
or, ∠ABD + ∠DBC = 90°
or, ∠DBC = 90° – ∠ABD
or, ∠DBC = 90° – 35° ...[From equation (ii)]
or, ∠DBC = 55°
Alternate Method: Since, the angle between chord and tangent is equal to the angle subtended by the same chord in alternate segment of the circle, Hence, ∠BDC = ∠BAD = 55°.
APPEARS IN
RELATED QUESTIONS
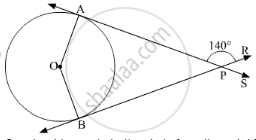
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
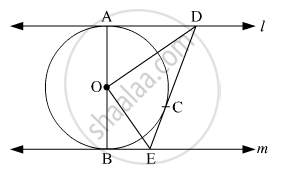
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
The length of the tangent from an external point P on a circle with centre O is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
The angle between two tangents to a circle may be 0°.
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
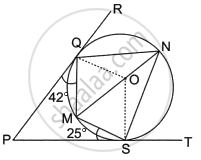
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
