Advertisements
Advertisements
Question
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

Solution
Given: Perimeter of ΔPQR = 20
i,e, PQ + QR + PR = 20
⇒ PQ + (QC + CR) + PR = 20
⇒ (PQ + QA) + (RB + PR) = 20 ...[∵ QA = QC and RC = RB as tangents from external points Q and R, respectively]
⇒ PA + PB = 20
⇒ PA + PA = 20 ...[∵ PA = PB as tangents from external point P]
⇒ 2PA = 20
⇒ PA = 10 cm
APPEARS IN
RELATED QUESTIONS
Find the area of the shaded region in Fig. 8, where \\

In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
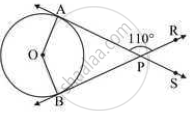
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.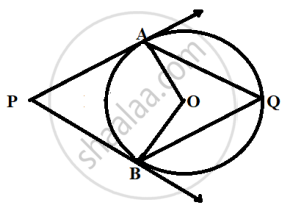
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
