Advertisements
Advertisements
प्रश्न
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

उत्तर
Given: Perimeter of ΔPQR = 20
i,e, PQ + QR + PR = 20
⇒ PQ + (QC + CR) + PR = 20
⇒ (PQ + QA) + (RB + PR) = 20 ...[∵ QA = QC and RC = RB as tangents from external points Q and R, respectively]
⇒ PA + PB = 20
⇒ PA + PA = 20 ...[∵ PA = PB as tangents from external point P]
⇒ 2PA = 20
⇒ PA = 10 cm
APPEARS IN
संबंधित प्रश्न
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
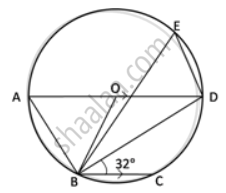
Find: ∠BED
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of tangent from an external point P on a circle with centre O is always less than OP.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
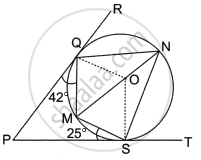
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
