Advertisements
Advertisements
प्रश्न
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
उत्तर
Draw a circle with centre O and take an external point P.
PA and PB are the tangents.
Join OP.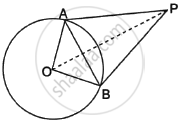
Now in ΔOAP and ΔOBP,
OA = OB ...(Radius of circle)
OP = OP ...(Common)
PA = PB ...(Tangents are equal)
So, by S.S.S criteria,
ΔOAP ≅ ΔOBP
So, ∠APO = ∠BPO
Hence, OP bisects ∠APB.
APPEARS IN
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
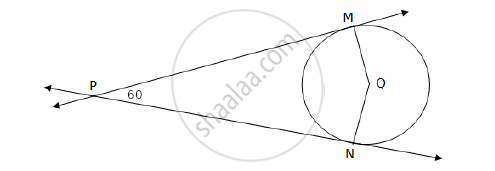
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.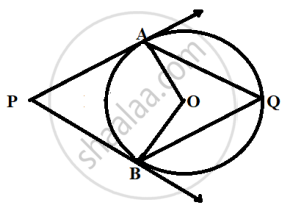
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
