Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.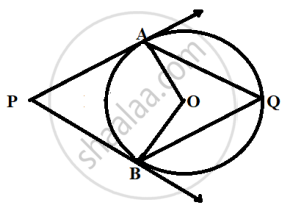
उत्तर
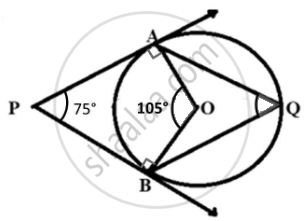
We know that
The radius is perpendicular to the tangent
∴ ∠OAP = ∠OBP = 90°
In quadrilateral PAOB
Sum of angles = 360°
∠APB + ∠OAP + ∠OBP + ∠AOB = 360°
75° + 90° + 90° + ∠AOB = 360°
255° + ∠AOB = 360°
∠AOB = 360° – 255°
∠AOB = 105°
Also, We know that
Angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the circle.
∴ ∠AOB = 2 × ∠AQB
105° = 2 × ∠AQB
2 × ∠AQB = 105°
∠AQB = `105^circ/2`
∠AQB = 52.5°
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
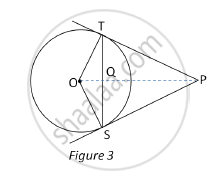
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
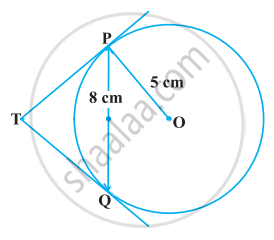
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
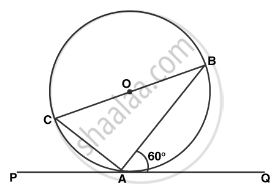
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
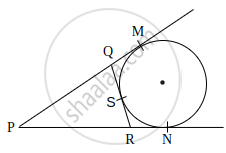
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
