Advertisements
Advertisements
प्रश्न
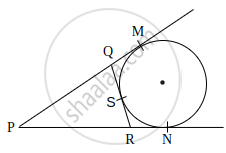
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
उत्तर

Given: A circle is touching a side QR of ΔPQR at point S.
PQ and PR are produced at M and N respectively.
To prove: PM = `1/2` (PQ + QR + PR)
Proof: PM = PN ...(i) (Tangents drawn from an external point P to a circle are equal)
QM = QS ...(ii) (Tangents drawn from an external point Q to a circle are equal)
RS = RN ...(iii) (Tangents drawn from an external point R to a circle are equal)
Now, 2PM = PM + PM
= PM + PN ...[From equation (i)]
= (PQ + QM) + (PR + RN)
= PQ + QS + PR + RS ...[From equations (i) and (ii)]
= PQ + (QS + SR) + PR
= PQ + QR + PR
∴ PM = `1/2` (PQ + QR + PR)
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Find the area of the shaded region in Fig. 8, where \\

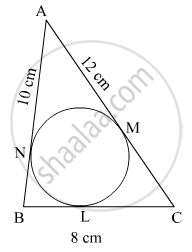
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

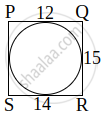
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.