Advertisements
Advertisements
प्रश्न
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
उत्तर १
Given: PA and PB are the tangent drawn from a point P to a circle with centre O. Also, the line segments OA and OB are drawn.

To Prove: ∠APB + ∠AOB = 180°
Proof: We know that the tangent to a circle is perpendicular to the radius through the point of contact.
Now, in right ΔOAP and right ΔOBP, we have PA = PB ...[Tangents to circle from an external point]
OA = OB ...[Radii of the same circle]
OP = OP ....[Common]
ΔOAP ≅ ΔOBP ....[by SSS congrurncy]
∠OPA = ∠OPB
and ∠AOP = ∠BOP
⇒ ∠APB = 2∠OPA and ∠AOB = 2∠AOP
In right ΔOAP
⇒ ∠AOP + ∠OPA + ∠PAO = 180°
⇒ ∠AOP = 180° − 90° − ∠OPA
⇒ ∠AOP = 90° − ∠OPA
⇒ 2∠AOP = 180° − 2∠OPA
⇒ ∠AOB = 180° − ∠APB
⇒ ∠AOB + ∠APB = 180°
उत्तर २

Let us consider a circle centered at point O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.
It can be observed that
OA (radius) ⊥ PA (tangent)
Therefore, ∠OAP = 90°
Similarly, OB (radius) ⊥ PB (tangent)
∠OBP = 90°
In quadrilateral OAPB,
Sum of all interior angles = 360º
∠OAP + ∠APB + ∠PBO + ∠BOA = 360º
90º + ∠APB + 90º + ∠BOA = 360º
∠APB + ∠BOA = 180º
Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
APPEARS IN
संबंधित प्रश्न
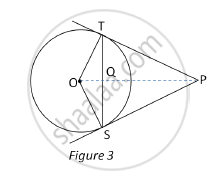
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°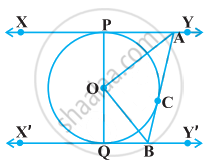
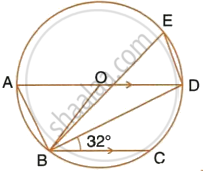
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
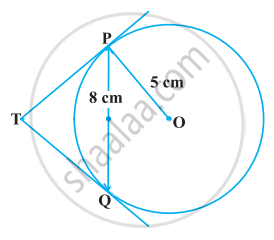
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
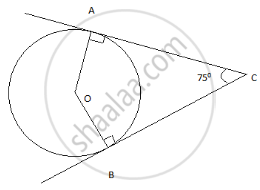
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

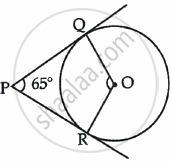
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
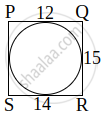
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.