Advertisements
Advertisements
प्रश्न
Prove that a parallelogram circumscribing a circle is a rhombus.
उत्तर
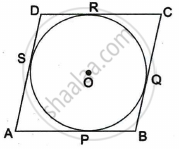
Let ABCD be the rhombus circumscribing the circle with centre O, such that AB, BC, CD and DA touch the circle at points P, Q, R and S respectively. We know that the tangents drawn to a circle from an exterior point are equal in length.
∴ AP = AS ...(i) [tangents from A]
BP = BQ ...(ii) [tangents from B]
CR = CQ ...(iii) [tangents from C]
DR = DS ...(iv) [tangents from D]
∴ AB + CD = AP + BP + CR + DR
= AS + BQ + CQ + DS ...[From (i), (ii), (iii), (iv)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, (AB + CD) = (AD + BC)
⇒ 2AB = 2AD
[∵ opposite sides of a parallelogram are equal]
⇒ AB = AD
∴ CD = AB = AD = BC
Hence, ABCD is a rhombus.
APPEARS IN
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

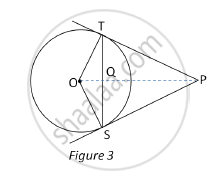
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
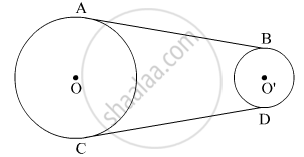
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
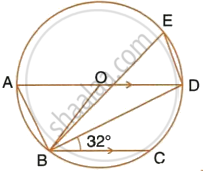
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
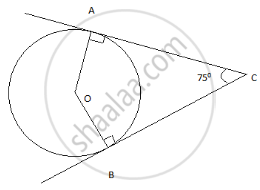
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
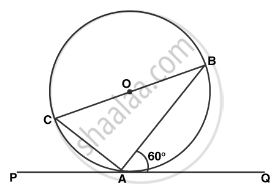
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
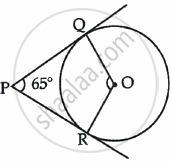
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.