Advertisements
Advertisements
प्रश्न
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
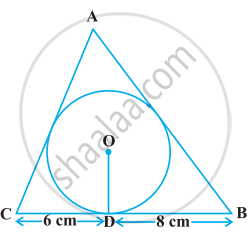
उत्तर
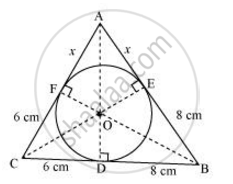
Let the given circle touch the sides AB and AC of the triangle at point E and F respectively and the length of the line segment AF be x.
In ΔABC,
CF = CD = 6cm ....(Tangents on the circle from point C)
BE = BD = 8cm ....(Tangents on the circle from point B)
AE = AF = x (Tangents on the circle from point A)
AB = AE + EB = x + 8
BC = BD + DC = 8 + 6 = 14
CA = CF + FA = 6 + x
2s = AB + BC + CA
= x + 8 + 14 + 6 + x
= 28 + 2x
s = 14 + x
`Area of triangleABC = sqrt(s(s-1)(s-b)(s-c))`
`=sqrt({14+x}{(14+x)-14}{(14+x)-(6+x)}{(14+x)-(8+x)})`
`=sqrt((14+x)(x)(8)(6))`
`=4sqrt(3(14x+x^2))`
`"Area of" triangleOBC = 1/2xxODxxBC`
` = 1/2xx4xx14`
`=28`
`"Area of" triangleOCA = 1/2xxOFxxAC`
` = 1/2xx4xx(6+x)`
` = 12+2x`
`"Area of" triangleOAB = 1/2xxOExxAB`
` = 1/2xx4xx(8+x) `
`=16+2x`
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
`4sqrt(3(14x+x^2)) = 28+12+2x+16+2x`
`4sqrt(3(14x+x^2)) = 56+4x`
`=>sqrt(3(14x+x^2)) = 14+x`
`=>3(14x+x^2) = (14+x)^2`
`=>42x+3x^2=196+x^2+28x`
`=>2x^2+14x-196 = 0`
`=>x^2+7x-98 = 0`
`=>x^2+14x-7x-98=0`
`=>x(x+14)-7(x+14) =0`
=>(x + 14) (x − 7) = 0
Either x + 14 = 0 or x − 7 = 0
Therefore, x = −14 and 7
However, x = −14 is not possible as the length of the sides will be negative.
Therefore, x = 7
Hence, AB = x + 8 = 7 + 8 = 15 cm
BC = 8 + 6 = 14 cm
CA = 6 + x = 6 + 7 = 13 cm
APPEARS IN
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
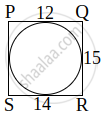
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
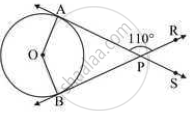
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of tangent from an external point P on a circle with centre O is always less than OP.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
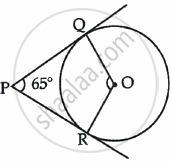
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.