Advertisements
Advertisements
Question
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
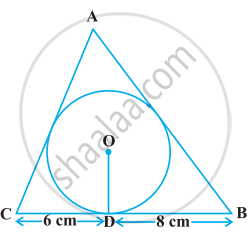
Solution
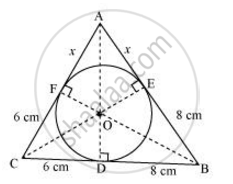
Let the given circle touch the sides AB and AC of the triangle at point E and F respectively and the length of the line segment AF be x.
In ΔABC,
CF = CD = 6cm ....(Tangents on the circle from point C)
BE = BD = 8cm ....(Tangents on the circle from point B)
AE = AF = x (Tangents on the circle from point A)
AB = AE + EB = x + 8
BC = BD + DC = 8 + 6 = 14
CA = CF + FA = 6 + x
2s = AB + BC + CA
= x + 8 + 14 + 6 + x
= 28 + 2x
s = 14 + x
`Area of triangleABC = sqrt(s(s-1)(s-b)(s-c))`
`=sqrt({14+x}{(14+x)-14}{(14+x)-(6+x)}{(14+x)-(8+x)})`
`=sqrt((14+x)(x)(8)(6))`
`=4sqrt(3(14x+x^2))`
`"Area of" triangleOBC = 1/2xxODxxBC`
` = 1/2xx4xx14`
`=28`
`"Area of" triangleOCA = 1/2xxOFxxAC`
` = 1/2xx4xx(6+x)`
` = 12+2x`
`"Area of" triangleOAB = 1/2xxOExxAB`
` = 1/2xx4xx(8+x) `
`=16+2x`
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
`4sqrt(3(14x+x^2)) = 28+12+2x+16+2x`
`4sqrt(3(14x+x^2)) = 56+4x`
`=>sqrt(3(14x+x^2)) = 14+x`
`=>3(14x+x^2) = (14+x)^2`
`=>42x+3x^2=196+x^2+28x`
`=>2x^2+14x-196 = 0`
`=>x^2+7x-98 = 0`
`=>x^2+14x-7x-98=0`
`=>x(x+14)-7(x+14) =0`
=>(x + 14) (x − 7) = 0
Either x + 14 = 0 or x − 7 = 0
Therefore, x = −14 and 7
However, x = −14 is not possible as the length of the sides will be negative.
Therefore, x = 7
Hence, AB = x + 8 = 7 + 8 = 15 cm
BC = 8 + 6 = 14 cm
CA = 6 + x = 6 + 7 = 13 cm
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
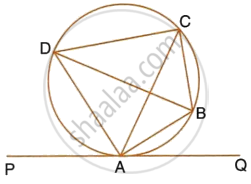
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
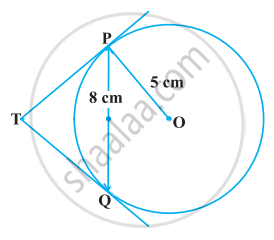
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
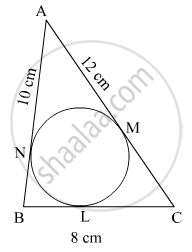
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point P on a circle with centre O is ______
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q such that OQ = 13 cm. Length PQ is ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
