Advertisements
Advertisements
Question
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

Solution
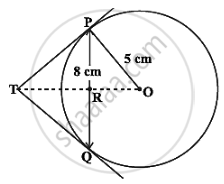
We know that tangents from an external point are equal in length, therefore TP = TQ
⇒ ΔTPQ is an isosceles triangle.
Also, we know that tangents from the external points are equally inclined to the segment.
∴ OT is bisector of ∠PTQ
⇒ OT ⊥ PQ ....[∵ In an isosceles triangle, angle bisector and altitude are the same]
⇒ ∠ORP = ∠TRP = 90°
Now, In ΔORP,
OR = `sqrt(5^2 - "PR"^2)`
= `sqrt(25 - 4^2)` .....[∵ Perpendicular from centre to a chord bisect the chord and so PR = RQ = 4 cm]
= `sqrt(25 - 16)`
= 3 cm
∵ ∠OPT = 90 .....[∵ Radius is ⊥ to the tangent at the point of contact]
∴ TP2 = OT2 – OP2 = (TR + 3)2 – 52 ...(i)
Also, from ΔPRT,
TP2 = PR2 + TR2 = 42 + TR2 ...(ii)
From equations (i) and (ii), we get
(TR + 3)2 – 52 = 42 + TR2
⇒ TR2 + 9 + 6TR – TR2 = 25 + 16 = 41
⇒ 6TR = 41 – 9 = 32
⇒ TR = `16/3`
Now, from equation (ii), we get
TP2 = `4^2 + (16/3)^2`
= `(16 xx 9 + 256)/9`
= `(144 + 256)/9`
= `400/9`
= `20/3`
TP = 6.67 cm
APPEARS IN
RELATED QUESTIONS
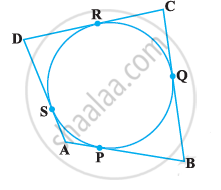
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°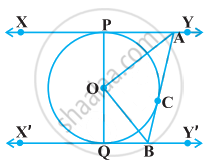
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
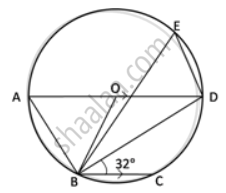
Find: ∠BED
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
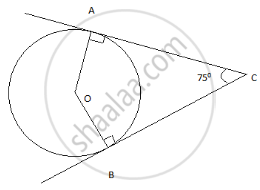
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.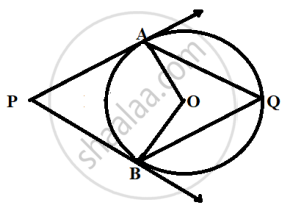
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
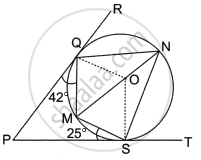
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
