Advertisements
Advertisements
प्रश्न
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

उत्तर
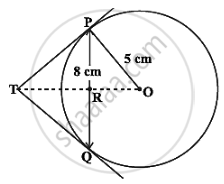
We know that tangents from an external point are equal in length, therefore TP = TQ
⇒ ΔTPQ is an isosceles triangle.
Also, we know that tangents from the external points are equally inclined to the segment.
∴ OT is bisector of ∠PTQ
⇒ OT ⊥ PQ ....[∵ In an isosceles triangle, angle bisector and altitude are the same]
⇒ ∠ORP = ∠TRP = 90°
Now, In ΔORP,
OR = `sqrt(5^2 - "PR"^2)`
= `sqrt(25 - 4^2)` .....[∵ Perpendicular from centre to a chord bisect the chord and so PR = RQ = 4 cm]
= `sqrt(25 - 16)`
= 3 cm
∵ ∠OPT = 90 .....[∵ Radius is ⊥ to the tangent at the point of contact]
∴ TP2 = OT2 – OP2 = (TR + 3)2 – 52 ...(i)
Also, from ΔPRT,
TP2 = PR2 + TR2 = 42 + TR2 ...(ii)
From equations (i) and (ii), we get
(TR + 3)2 – 52 = 42 + TR2
⇒ TR2 + 9 + 6TR – TR2 = 25 + 16 = 41
⇒ 6TR = 41 – 9 = 32
⇒ TR = `16/3`
Now, from equation (ii), we get
TP2 = `4^2 + (16/3)^2`
= `(16 xx 9 + 256)/9`
= `(144 + 256)/9`
= `400/9`
= `20/3`
TP = 6.67 cm
APPEARS IN
संबंधित प्रश्न
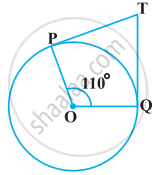
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
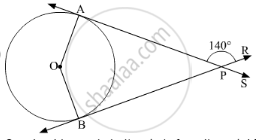
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
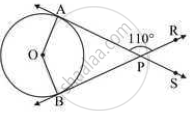
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
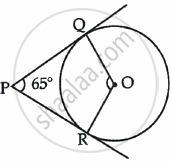
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
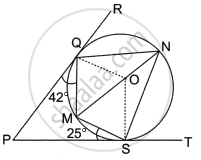
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
