Advertisements
Advertisements
प्रश्न
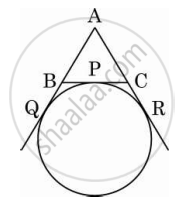
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
उत्तर
Given, circle touching the side BC of ΔABC at point P and AB, AC produced at Q and R, respectively.
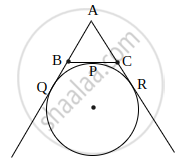
We know, lengths of tangents drawn from on external point to a circle are equal.
∴ AQ = AR ...(i)
BQ = BP ...(ii)
CP = CR ...(iii)
Perimeter of ΔABC = AB + BC + CA
=AB + (BP + PC) + (AR – CR)
= (AB + BP) + PC + (AQ – CP) ...[From equations (i) and (ii)]
= (AB + BQ) + PC + (AQ – CP) ...[From equation (ii)]
= AQ + PC + AQ – PC
= 2AQ
∴ AQ = `1/2` (perimeter of ΔABC)
APPEARS IN
संबंधित प्रश्न
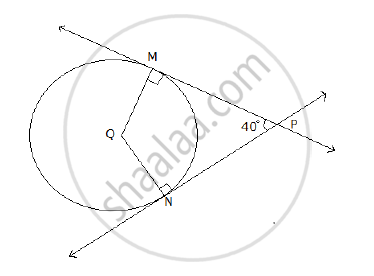
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
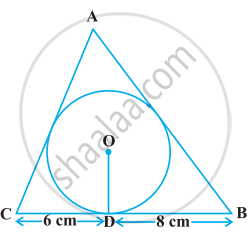
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
The length of the tangent from an external point P on a circle with centre O is ______
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

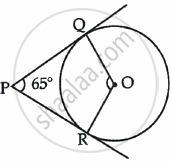
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
