Advertisements
Advertisements
प्रश्न
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
उत्तर
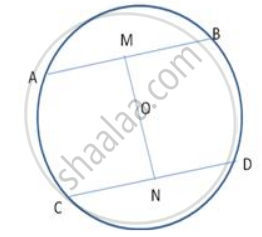
AM = MB
CN = ND
∴ OM ⊥ AB
and ON ⊥ CD
(A line bisecting the chord and passing through the centre of the circle is perpendicular to the chord)
∴ ∠ OMA = ∠ OND = 90° each
But these are alternate interior angles
∴ AB || CD
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
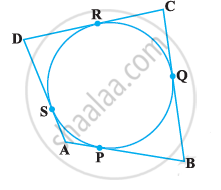
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Prove that a parallelogram circumscribing a circle is a rhombus.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
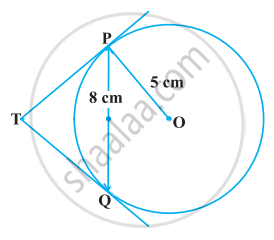
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
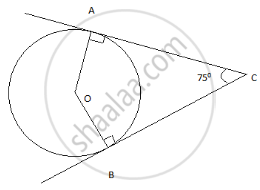
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
The angle between two tangents to a circle may be 0°.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

