Advertisements
Advertisements
प्रश्न
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
उत्तर
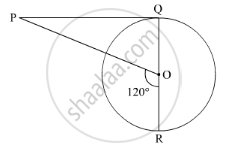
Given: PQ is the tangent to the circle with centre O. QOR is the diameter.
In\[∆ POQ\]
\[ \Rightarrow \angle OPQ = 120^o - 90^o = 30^o\]
APPEARS IN
संबंधित प्रश्न
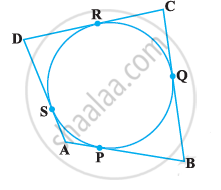
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
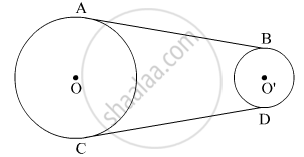
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
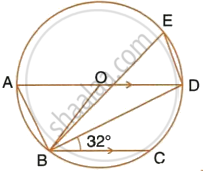
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
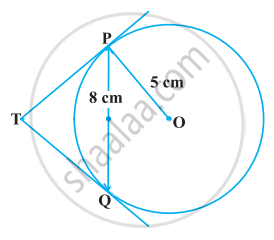
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
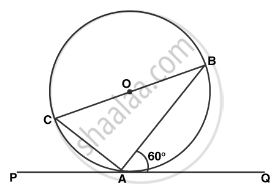
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
