Advertisements
Advertisements
प्रश्न
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
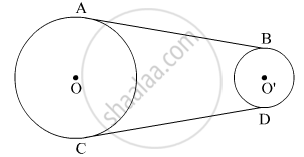
उत्तर १
Construct a line passing through AD
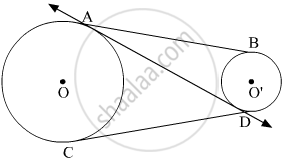
Now, AD and CD are tangents to the circle with centre O from the external point D.
So, AD = CD (Tangents drawn from an external point to a circle are equal) ...(1)
Also, AB and AD are the tangents to the circle with centre O' from the external point A.
So, AD = AB (Tangents drawn from an external point to a circle are equal) ...(2)
From (1) and (2)
AB = CD
Hence proved.
उत्तर २
Given: AB and CD are two common tangents to two circles of unequal radii.
To Prove: AB = CD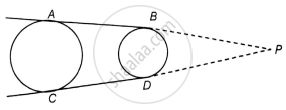
Construction: Produce AB and CD, to intersect at P.
Proof: Consider the circle with greater radius.
AP = CP ...[Tangents drawn from an external point to a circle are equal] [1]
Also, Consider the circle with smaller radius.
BP = BD ...[Tangents drawn from an external point to a circle are equal] [2]
Substract [2] from [1], we get
AP – BP = CP – BD
AB = CD
Hence proved.
संबंधित प्रश्न
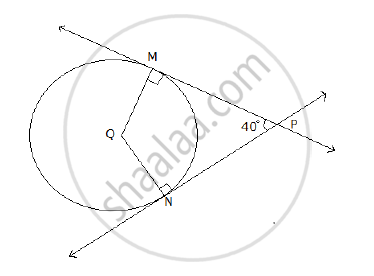
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
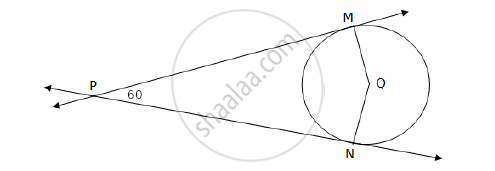
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
The length of the tangent from an external point on a circle is ______
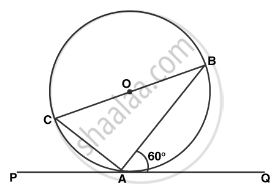
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

