Advertisements
Advertisements
प्रश्न
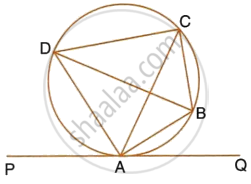
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
उत्तर
∠CAB = ∠BAQ = 30° ...(AB is angle bisector of ∠CAQ)
∠CAQ = 2∠BAQ = 60° ...(AB is angle bisector of ∠CAQ)
∠CAQ + ∠PAC = 180° ...(angles in linear pair)
∴ ∠PAC = 120°
∠PAC = 2∠CAD ...(AD is angle bisector of ∠PAC)
∠CAD = 60°
Now,
∠CAD + ∠CAB = 60° + 30° = 90°
∠DAB = 90°
Thus, BD subtends 90° on the circle
So, BD is the diameter of circle
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure PA = 6, PB = 4 and PC = 8. Find PD
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.