Advertisements
Advertisements
प्रश्न
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

उत्तर
In a cyclic quadrilateral ABCD,
`∠ ABC+∠ADC=180°` (Opposite angle of a cydic quadrilateral are supplementary)
`⇒ 100°+∠ADC=180°`
`⇒ ∠ADC=80°`
Now, in `ΔACD`,
`∠ADC+∠CAD+∠ADC=180°`
`⇒40°+∠CAD+80°=180°`
`⇒∠CAD=180°-120°`
`⇒∠CAD=60°`
`"Now" ∠DCT=∠CAD ...........("angles in the alternate segment are equal")`
`∴ ∠DCT=60°`
APPEARS IN
संबंधित प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
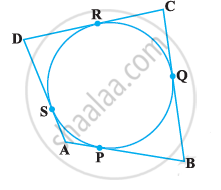
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
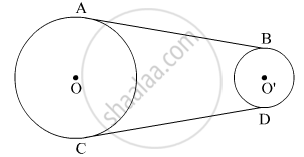
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
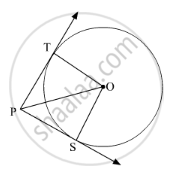
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
The length of the tangent from an external point on a circle is ______
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
