Advertisements
Advertisements
प्रश्न
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
उत्तर
Let us draw the circle with external point P and two tangents PQ and PR.

We know that the radius is perpendicular to the tangent at the point of contact.
∴∠OQP=90°
We also know that the tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point.
∴∠QPO=60°
Now in ∆QPO:
`cos60^@="PQ"/"PO"`
`⇒1/2="PQ"/"PO"`
`⇒2PQ=PO`
APPEARS IN
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Find the area of the shaded region in Fig. 8, where \\

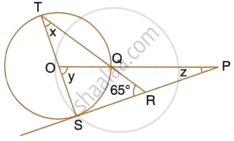
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
The length of tangents drawn from an external point to the circle ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The angle between two tangents to a circle may be 0°.
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.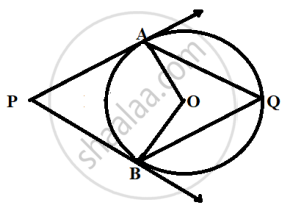
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
