Advertisements
Advertisements
प्रश्न
Find the area of the shaded region in Fig. 8, where \\

उत्तर
Area of the shaded region
= Area of the semicircle with diameter AD + Area of the semicircle with diameter BC
− Area of the semicircle with diameter AB − Area of the semicircle with diameter CD
\[= \frac{1}{2}\pi \left( \frac{14}{2} \right)^2 + \frac{1}{2}\pi \left( \frac{7}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 \]
\[ = \frac{1}{2} \times \frac{22}{7} \times \left( \frac{3 . 5}{2} \right)^2 \times \left[ 16 + 4 - 1 - 1 \right]\]
\[ = \frac{1}{2} \times \frac{22}{7} \times \frac{3 . 5}{2} \times \frac{3 . 5}{2} \times 18\]
\[ = 86 . 625 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
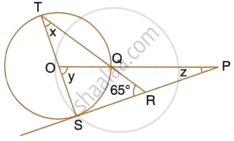
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The length of tangents drawn from an external point to the circle ______
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.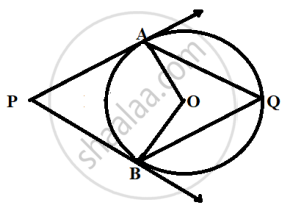
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
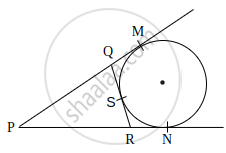
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

