Advertisements
Advertisements
प्रश्न
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
उत्तर
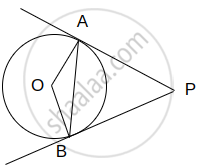
Let us draw the circle with external point P and two tangents PQ and PR.

We know that the radius is perpendicular to the tangent at the point of contact.
∴∠OQP=90°
We also know that the tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point.
∴∠QPO=60°
Now in ∆QPO:
`cos60^@="PQ"/"PO"`
`⇒1/2="PQ"/"PO"`
`⇒2PQ=PO`
APPEARS IN
संबंधित प्रश्न
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
Find the area of the shaded region in Fig. 8, where \\

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
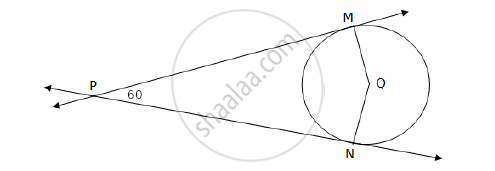
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
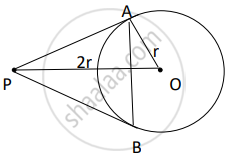
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
The length of tangent from an external point P on a circle with centre O is always less than OP.
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.