Advertisements
Advertisements
प्रश्न
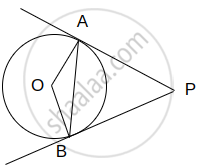
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.
उत्तर
∠OAB = 30°
∠OAP = 90° ...[Angle between the tangent and the radius at the point of contact]
∠PAB = 90° – 30° = 60°
AP = BP ...[Tangents to a circle from an external point]
∠PAB = ∠PBA ...[Angles opposite to equal sides of a triangle]
In ΔABP, ∠PAB + ∠PBA + ∠APB = 180° ...[Angle Sum Property]
60° + 60° + ∠APB = 180°
∠APB = 60°
∴ ΔABP is an equilateral triangle, where AP = BP = AB.
PA = 6 cm
In Right ΔOAP, ∠OPA = 30°
tan 30° = `(OA)/(PA)`
`1/sqrt(3) = (OA)/6`
OA = `6/sqrt(3) = 2sqrt(3)cm`
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
The length of the tangent from an external point P on a circle with centre O is ______
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
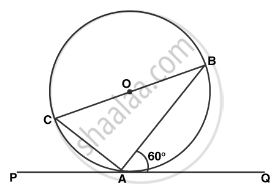
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
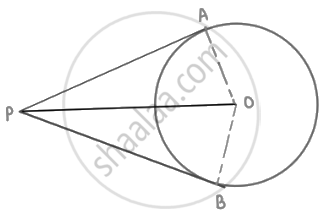
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
