Advertisements
Advertisements
प्रश्न
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
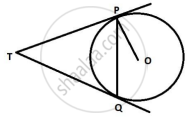
उत्तर १
Given: A circle with centre O and an external point T from which tangents TP and TQ are drawn to touch the circle at P and Q.
To prove: ∠PTQ = 2∠OPQ.
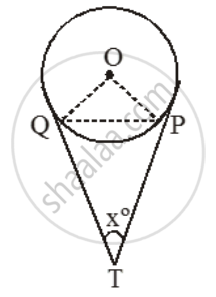
Proof: Let ∠PTQ = xº. Then,
∠TQP + ∠TPQ + ∠PTQ = 180º
[∵ sum of the ∠s of a triangle is 180º]
⇒ ∠TQP + ∠TPQ = (180º – x) ….(i)
We know that the lengths of tangent drawn from an external point to a circle are equal.
So, TP = TQ.
Now, TP = TQ
⇒ ∠TQP = ∠TPQ
`=\frac{1}{2}(180^{0}-x)=( 90^\text{o}-\frac{x}{2})`
∴ ∠OPQ = (∠OPT–∠TPQ)
`=90^{0}-( 90^\text{o}-\frac{x}{2})=\frac{x}{2} `
`⇒ ∠OPQ = \frac { 1 }{ 2 } ∠PTQ`
⇒ 2∠OPQ = ∠PTQ
उत्तर २
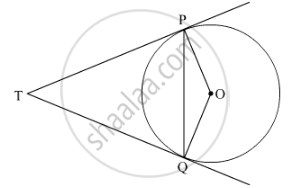
Given: TP and TQ are two tangents of a circle with centre O and P and Q are points of contact
To prove: ∠PTQ = 2∠OPQ
Suppose ∠PTQ = θ.
Now by theorem, "The lengths of a tangents drawn from an external point to a circle are equal".
So, TPQ is an isoceles triangle.
Therefore, ∠TPQ = ∠TQP = `1/2`(180°− θ) = 90°−`θ/2`.
Also by theorem "The tangents at any point of a circle is perpendicular to the radius through the point of contact" ∠OPT = 90°.
Therefore,
∠OPQ = ∠OPT − ∠TPQ
`= 90^@ - (90^@ - 1/2theta)`
`= 1/2 theta`
= `1/2` ∠PTQ
Hence, 2∠OPQ = ∠PTQ.
APPEARS IN
संबंधित प्रश्न
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

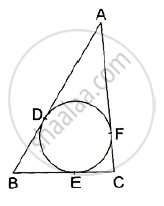
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
In the given figure, O is the centre of the circle. Name all chords of the circle.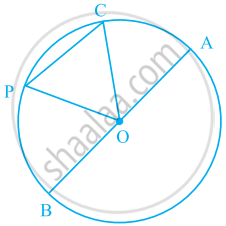
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
