Advertisements
Advertisements
प्रश्न
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
उत्तर
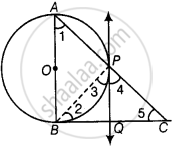
According to the question,
In a right angle ΔABC is which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P.
Also PQ is a tangent at P
To Prove: PQ bisects BC i.e. BQ = QC
Proof: ∠APB = 90° ...[Angle in a semicircle is a right-angle]
∠BPC = 90° ...[Linear Pair]
∠3 + ∠4 = 90° ...[1]
Now, ∠ABC = 90°
So in ΔABC
∠ABC + ∠BAC + ∠ACB = 180°
90° + ∠1 + ∠5 = 180°
∠1 + ∠5 = 90° ...[2]
Now, ∠1 = ∠3 ...[Angle between tangent and the chord equals angle made by the chord in alternate segment]
Using this in [2] we have
∠3 + ∠5 = 90° ...[3]
From [1] and [3] we have
∠3 + ∠4 = ∠3 + ∠5
∠4 = ∠5
QC = PQ ...[Sides opposite to equal angles are equal]
But also, PQ = BQ ...[Tangents drawn from an external point to a circle are equal]
So, BQ = QC
i.e. PQ bisects BC.
संबंधित प्रश्न
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the given figure, O is the centre of the circle. Find ∠CBD.

Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Find the area of a circle of radius 7 cm.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Draw circle with the radii given below.
3 cm
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.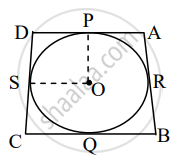
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
