Advertisements
Advertisements
प्रश्न
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.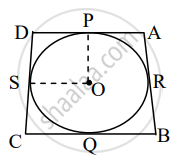
उत्तर
Given: AD ⊥ DC
BC = 38, QB = 27, DC = 25
To find: Radius of the circle, i.e., OP.
Solution:
BC = 38 ......[Given]
∴ BQ + QC = 38 ......[B–Q–C]
∴ 27 + QC = 38 .......[Given]
∴ QC = 38 – 27
∴ QC = 11 units ......(i)
Now, QC = SC ......[Tangent segment theorem]
∴ SC = 11 units .....(ii) [From (i)]
DC = 25 .......[Given]
∴ DS + SC = 25 ......[D–S–C]
∴ DS + 11 = 25 ......[From (ii)]
∴ DS = 25 – 11
∴ DS = 14 units ......(iii)
In ▢DSOP,
∠P = ∠S = 90° ......[Tangent theorem]
∠D = 90° ......[Given]
∴ ∠O = 90° ......[Remaning angle of ▢DSOP]
∴ ▢DSOP is a rectangle.
Also, OP = OS ......[Radii of the same circle]
∴ ▢DSOP is a square .......`[("A rectangle is square if its"),("adjacent sides are congruent")]`
∴ OS = DS = DP = PO .....(iv) [Sides of the square]
∴ OP = 14 units ......[From (iii) and (iv)]
∴ The radius of the circle is 14 units.
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at center.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
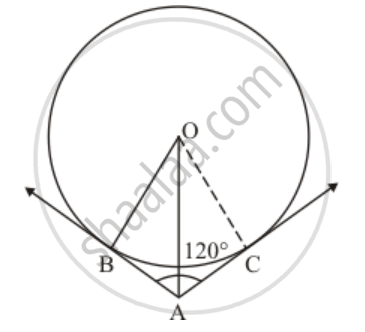
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
From the figure, identify a sector.

