Advertisements
Advertisements
प्रश्न
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
उत्तर
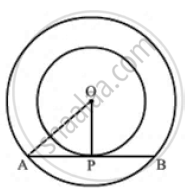
We know that the radius and tangent are perpendicular at their point of contact since the perpendicular drawn from the centre bisects the chord.
∴ AP = PB = `(AB)/2` = 4 cm
In the right triangle, AOP
AO2 = OP2 + PA2
⇒ 52 = OP2 + 42
⇒ OP2 = 9
⇒ OP = 3 cm
Hence, the radius of the smaller circle is 3 cm.
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Can the length of a chord of a circle be greater than its diameter ? Explain.
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

From the figure, identify a sector.

A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.