Advertisements
Advertisements
प्रश्न
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.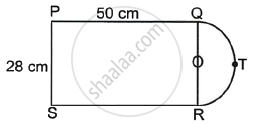
उत्तर
Given: The rectangle is PQRS, and the semi-circle is OQTR, both drawn on side QR.
Now, Area of the rectangle PQRS = 50 × 28 = 1400 cm2
Radius of the semi-circle, r = `(QR)/2 = 28/2` = 14 cm
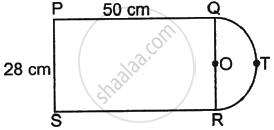
So, Area of semi-circle OQTR = `1/2 πr^2`
= `1/2 xx 22/7 xx (14)^2`
= `1/2 xx 22/7 xx 14 xx 14`
= 22 × 14
= 308 cm2
Area of the plot = Area of semi-circle OQTR + Area of rectangle PQRS
= 308 + 1400
= 1708 cm2
As a result, the plot's area is 1708 cm2.
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
The ratio between the circumference and diameter of any circle is _______
Find the diameter of the circle
Radius = 8 cm
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
In the given figure, O is the centre of the circle. Name all radii of the circle.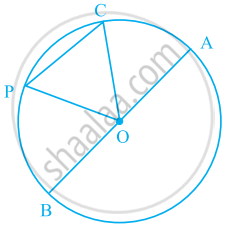
From the figure, identify two points in the interior.

