Advertisements
Advertisements
Question
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.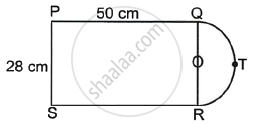
Solution
Given: The rectangle is PQRS, and the semi-circle is OQTR, both drawn on side QR.
Now, Area of the rectangle PQRS = 50 × 28 = 1400 cm2
Radius of the semi-circle, r = `(QR)/2 = 28/2` = 14 cm
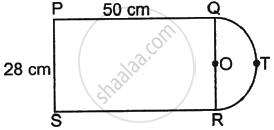
So, Area of semi-circle OQTR = `1/2 πr^2`
= `1/2 xx 22/7 xx (14)^2`
= `1/2 xx 22/7 xx 14 xx 14`
= 22 × 14
= 308 cm2
Area of the plot = Area of semi-circle OQTR + Area of rectangle PQRS
= 308 + 1400
= 1708 cm2
As a result, the plot's area is 1708 cm2.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
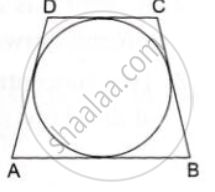
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
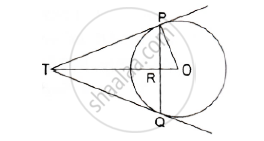
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
Twice the radius is ________________
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
