Advertisements
Advertisements
Question
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Solution
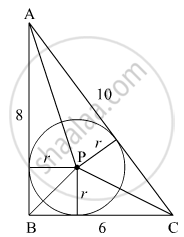
We have given that a circle is inscribed in a triangle
Using pythagoras theorem
`(AC)^2 = (AB)^2 + (BC)^2`
`(AC)^2 = (8)^2 + (6)^2`
`(AC)^2 = 64 + 36`
`(AC)^2 = 100`
⇒ AC = 10
Area of Δ ABC = area of Δ APB + area of Δ BPC + area of Δ APC
`1/2 xx b xx h = 1/2 xx b_1 xx h_1 + 1/2 xx b_2 xx h_2 + 1/2 xx b_3 xx h_3`
`1/2 xx 6 xx 8 = 1/2 xx 8 xx r + 1/2 xx 6 xx r + 1/2 xx 10 xx r`
`24 = 4r + 3r + 5r`
`24 = 12r`
⇒ r = 2
∵ d = 2r
⇒ `d = 2 xx 2`
⇒ d = 4 cm
APPEARS IN
RELATED QUESTIONS
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
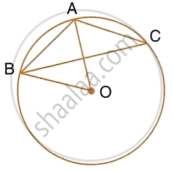
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.