Advertisements
Advertisements
Question
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
Solution
Given: PQ is the diameter of the circle.
Point P, Q, C are points of contact of the respective tangents.
To prove: ∠AOB = 90°
Construction: Draw seg OC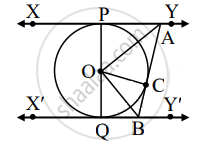
Proof:
In ∆OPA and ∆OCA,
side OP ≅ side OC ......[Radii of the same circle]
side OA ≅ side OA ......[Common side]
side PA ≅ side CA ......[Tangent segment theorem]
∴ ∆OPA ≅ ∠OCA .....[[SSS test of congruency]
∴ ∠AOP ≅ ∠AOC ......[C.A.C.T.]
Let m∠AOP = m∠AOC = x ......(i)
Similarly, we can prove that ∠BOC ≅ ∠BOQ.
Let m∠BOC = m∠BOQ = y ......(ii)
m∠AOP + m∠AOC + m∠BOC + m∠BOQ = 180° .....[Linear angles]
∴ x + x + y + y = 180° ......[From (i) and (ii)]
∴ 2x + 2y = 180°
∴ 2(x + y) = 180°
∴ x + y = 90° ......(iii)
Now ∠AOB = ∠AOC + ∠BOC
= x + y ......[From (i) and (ii)]
∴ ∠AOB = ∠AOC + ∠BOC
= x + y
∴ ∠AOB = 90° .....[From (iii)]
APPEARS IN
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
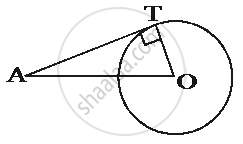
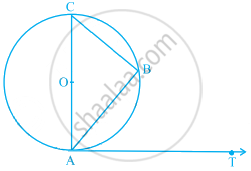
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure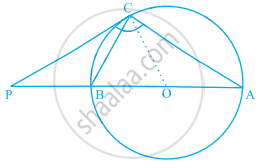
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
