Advertisements
Advertisements
Question
The chords AB and CD of the circle intersect at point M in the interior of the same circle then prove that CM × BD = BM × AC
Solution
Given: Chords AB and CD intersect at point M.
To prove: CM × BD = BM × AC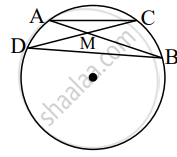
Proof: In ∆AMC and ∆DMB,
∠AMC ≅ ∠DMB ......[Vertically opposite angles]
∠ACD ≅ ∠ABD ......[Angles inscribed in the same arc]
∴ ∆AMC ∼ ∆DMB ......[AA test of similarity]
∴ `"CM"/"BM" = "AC"/"BD"` .....[Corresponding sides of similar triangles]
∴ CM × BD = BM × AC
APPEARS IN
RELATED QUESTIONS
In the given figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠ RTS is an acute angle.
In the given figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).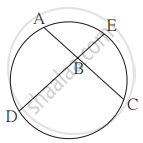
In the given figure, if PQ = 6, QR = 10, PS = 8 find TS.
∠ACB is inscribed in arc ACB of a circle with centre O. If ∠ACB = 65°, find m(arc ACB).
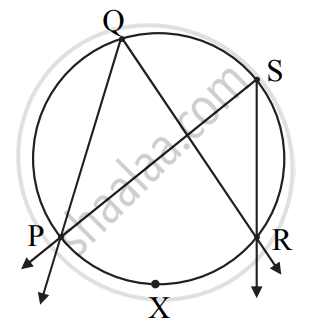
Prove that, angles inscribed in the same arc are congruent.
Given: ∠PQR and ∠PSR are inscribed in the same arc
Arc PXR is intercepted by the angles.
To prove: ∠PQR ≅ ∠PSR
Proof :
m∠PQR = `1/2` m(arc PXR) .......(i) `square`
m∠`square` = `1/2` m(arc PXR) ......(ii) `square`
∴ m∠`square` = m∠PSR .......[From (i) and (ii)]
∴ ∠PQR ≅ ∠PSR ........(Angles equal in measure are congruent)
In the figure, two chords AB and CD of the same circle are parallel to each other. P is the centre of the circle. show that ∠CPA = ∠DPB.

Construct the incircle of Δ RST in which RS = 6cm, ST 7 cm, RT
= 6.5 cm.
Four alternative answers for the following question is given. Choose the correct alternative.
What is the measurement of angle inscribed in a semicircle?
In the figure if ∠PQR = 50°, then find ∠PSR.
In the figure, if ∠ABC = 35°, then find m(arc AXC)?