Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Solution
In the given figure, let us join D an A.

Consider `ΔOCA`. We have,
OC = OA (Radii of the same circle)
We know that angles opposite to equal sides of a triangle will be equal. Therefore,
`∠OCA =∠OAC ` … (1)
It is clear from the figure that
`∠DCA +∠OCA=∠OCD`
Now from (1)
`∠DCA +∠OAC =∠OCD`
Now as BD is tangent therefore, `∠OCD=90^circ.`
Therefore `∠DCA +∠OAC = 90^circ`
From the figure we can see that `∠OAC =∠BAC`
`∠DAC + ∠BAC = 90^o`
Thus, we have proved.
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
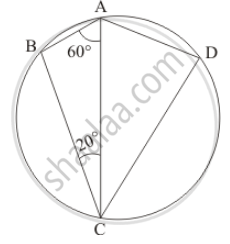
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
The circumcentre of a triangle is the point which is ______.
