English Medium
Academic Year: 2024-2025
Date & Time: 10th March 2025, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions very carefully and strictly follow them:
- This question paper contains 38 questions. All questions are compulsory.
- This question paper is divided into five Sections - A, B, C, D and E.
- In Section A, Questions no. 1 to 18 are multiple choice questions (MCQs) and questions number 19 and 20 are Assertion-Reason based questions of 1 mark each.
- In Section B, Questions no. 21 to 25 are very short answer (VSA) Lype questions, carrying 2 marks each.
- In Section C, Questions no. 26 to 31 are short answer (SA) type questions, carrying 3 marks cach.
- In Section D, Questions no. 32 to 35 are long answer (LA) type questions carrying 5 marks each.
- In Section E, Questions no. 36 to 38 are case study based questions carrying 4 marks each. Internal choice is provided in 2 marks questions in each case study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
- Draw neat diagrams wherever required. Take `pi = 22/7` wherever required,
if not stated. - Use of calculator is not allowed.
What is the mode of a data if median and mean of the same data are 9.6 and 10.5, respectively?
7.8
12.3
8.4
7
Chapter:
The value of (tan A cosec A)2 − (sin A sec A)2 is ______.
0
1
−1
2
Chapter:
A kite is flying at a height of 150 m from the ground. It is attached to a string inclined at an angle of 30° to the horizontal. The length of the string is ______.
`100 sqrt3` m
300 m
`150 sqrt 2` m
`150 sqrt3` m
Chapter:
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
congruent but not similar
similar but not congruent
neither congruent nor similar
congruent as well as similar
Chapter: [0.040999999999999995] Triangles
If θ is an acute angle and 7 + 4 sin θ = 9, then the value of θ is ______.
90°
30°
45°
60°
Chapter:
Two polynomials are shown in the graph below. The number of distinct zeroes of both the polynomials is ______.
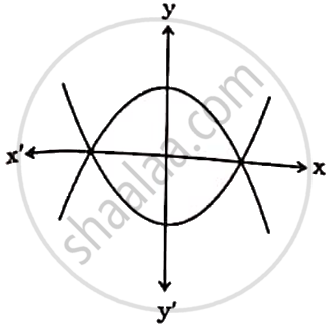
3
5
2
4
Chapter:
In the given figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB = 115°, then ∠APO is equal to ______.
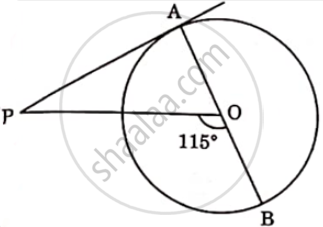
25°
65°
90°
35°
Chapter:
A piece of wire 20 cm long is bent into the form of an arc of a circle of radius `60/pi` cm. The angle subtended by the arc at the centre of the circle is ______.
30°
60°
90°
50°
Chapter:
If HCF(98, 28) = m and LCM(98, 28) = n, then the value of n - 7m is ______.
0
28
98
196
Chapter:
Which of the following is a rational number between `sqrt3` and `sqrt5`?
1.4142387954012...
`2.32bar6`
π
1.857142
Chapter:
The sum of the zeroes of the polynomial p(x) = 5x − 7x2 + 3 is ______.
`(-7)/5`
`7/5`
`5/7`
`(-5)/7`
Chapter:
If x = 1 and y = 2 is a solution of the pair of linear equations 2x − 3y + a = 0 and 2x + 3y − b = 0, then ______.
a = 2b
2a = b
a + 2b = 0
2a + b = 0
Chapter:
If sector of a circle has an area of 40π sq units and a central angle of 72°, the radius of the circle is ______.
200 units
100 units
20 units
`10sqrt2` units
Chapter:
The tangents drawn at the extremities of the diameter of a circle are ______.
perpendicular
parallel
equal
intersecting
none of these
Chapter: [0.042] Circles
If (−1)n + (−1)8 = 0, then n is ______.
any positive integer
any negative integer
any odd number
any even number
Chapter:
The end points of a diameter of circle are (2, 4) and (−3, −1). The length of its radius is ______.
`(5sqrt2)/2` units
`5sqrt2` units
`3sqrt2` units
`+- (5sqrt2)/2` units
Chapter:
The 11th and 13th term of an AP are 39 and 45, respectively. What is the common difference of the AP?
42
21
6
3
Chapter:
Advertisements
A card is drawn at random from a pack of 52 cards. What is the probability that the card drawn is a spade or a king?
`1/13`
`2/13`
`4/13`
`9/13`
Chapter:
Assertion (A): The probability of selecting a number at random from the numbers 1 to 20 is 1.
Reason (R): For any event E, if P(E) = 1, then E is called a sure event.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
Assertion (A): If we join two hemispheres of same radius along their bases, then we get a sphere.
Reason (R): Total Surface Area of a sphere of radius r is 3rr2.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
If ΔABC ~ ΔPQR in which AB = 6 cm, BC = 4 cm, AC = 8 cm and PR = 6 cm, then find the length of (PQ + QR).
Chapter:
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

Chapter: [0.040999999999999995] Triangles
If x cos 60° + y cos 0° + sin 30° − cot 45° = 5, then find the value of x + 2y.
Chapter:
Evaluate:
`(tan^2 60^@)/(sin^2 60^@ + cos^2 30^@)`
Chapter:
A person is standing at P outside a circular ground at a distance of 26 m from the centre of the ground. He found that his distances from the points A and B on the ground are 10 m (PA and PB are tangents to the circle). Find the radius of the circular ground.
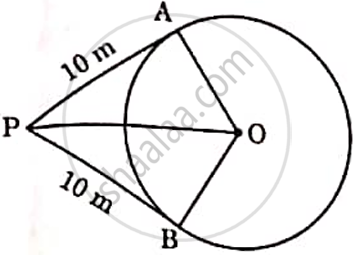
Chapter:
Find the zeroes of the polynomial p(x) = `x^2 + 4/3x − 4/3`.
Chapter:
Find the length of the median through the vertex B of ΔABC with vertices A(9, −2), B(−3, 7) and C(−1, 10).
Chapter:
Prove that `sqrt(5)` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Two dice are rolled together. Find the probability of getting a multiple of 2 on one and a multiple of 3 on the other die.
Chapter:
Two dice are rolled together. Find the probability of getting the product of two numbers on the top of the two dice is a perfect square number.
Chapter:
Advertisements
Prove that:
`tan theta/(1 - cot theta) + cot theta/(1 - tan theta)` = 1 + sec θ cosec θ
Chapter:
Prove that:
`(sin A + cos A)/(sin A - cos A) + (sin A - cos A)/(sin A + cos A) = 2/(2 sin^2 A - 1)`
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
A room is in the form of a cylinder surmounted by a hemispherical dome. The base radius of the hemisphere is half of the height of the cylindrical part. If the room contains `1408/21 m^3` of air, find the height of the cylindrical part. `("Use" pi = 22/7)`
Chapter:
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Chapter: [0.042] Circles
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Chapter: [0.042] Circles
Find the ratio in which the y-axis divides the line segment joining the points (5, −6) and (−1, −4). Also, find the point of intersection.
Chapter:
The perimeter of a right triangle is 60 cm and its hypotenuse is 25 cm. Find the lengths of other two sides of the triangle.
Chapter:
Represent the following situation in the form of a quadratic equation.
A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Chapter: [0.023] Quadratic Equations
A bag contains some red and blue balls. Ten percent of the red balls, when added to twenty percent of the blue balls, give a total of 24. If three times the number of red balls exceeds the number of blue balls by 20, find the number of red and blue balls.
Chapter:
The lengths of 40 leaves of a plant are measured correct to the nearest millimeter, and the data obtained is represented in the following table:
| Length (in mm) | Number of leaves |
| 118 − 126 | 3 |
| 127 – 135 | 5 |
| 136 − 144 | 9 |
| 145 – 153 | 12 |
| 154 – 162 | 5 |
| 163 – 171 | 4 |
| 172 – 180 | 2 |
Find the median length of the leaves.
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 − 126.5, 126.5 − 135.5… 171.5 − 180.5)
Chapter: [0.071] Statistics
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
Amrita stood near the base of a lighthouse, gazing up at its towering height. She measured the angle of elevation to the top and found it to be 60°. Then she climbed a nearby observation deck. 40 metres higher than her original position and noticed the angle of elevation to the top of lighthouse to be 45°.

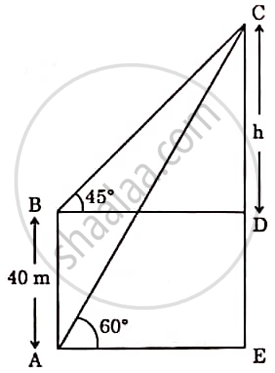
Based on the above given information, answer the following questions:
(i) If CD is h metres, find the distance BD in terms of 'h'.
(ii) Find distance BC in terms of 'h'.
(iii) (a) Find the height CE of the lighthouse [Use `sqrt3` = 1.73]
OR
(iii) (b) Find distance AE, if AC = 100m.
Chapter:
A school is organizing a charity run to raise funds for a local hospital. The run is planned as a series of rounds around a track. with each round being 300 metres. To make the event more challenging and engaging. the organizers decide to increase the distance of each subsequent round by 50 metres. For example, the second round will be 350 metres, the third round will be 400 metres and so on. The total number of rounds planned is 10.

Based on the information given above, answer the following questions:
- Write the fourth, fifth, and sixth terms of the Arithmetic Progression so formed.
- Determine the distance of the 8th round. (1)
-
- Find the total distance run after completing all 10 rounds. (2)
OR - If a runner completes only the first 6 rounds, what is the total distance run by the runner? (2)
- Find the total distance run after completing all 10 rounds. (2)
Chapter:
A brooch is a decorative piece often worn on clothing like jackets, blouses or dresses to add elegance. Made from precious metals and decorated with gemstones, brooches come in many shapes and designs.

One such brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the figure.
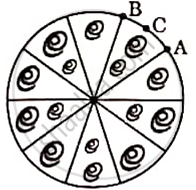
Based on the above given information, answer the following questions:
(i) Find the central angle of each sector. (1)
(ii) Find the length of the arc ACB. (1)
(iii) (a) Find the area of each sector of the brooch. (2)
OR
(iii) (b) Find the total length of the silver wire used. (2)
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CBSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
