Question

A brooch is a decorative piece often worn on clothing like jackets, blouses or dresses to add elegance. Made from precious metals and decorated with gemstones, brooches come in many shapes and designs.

One such brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the figure.

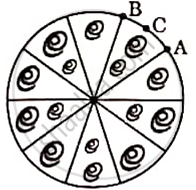
Based on the above given information, answer the following questions:

(i) Find the central angle of each sector.       (1)

(ii) Find the length of the arc ACB.      (1)

(iii) (a) Find the area of each sector of the brooch.      (2)

OR

(iii) (b) Find the total length of the silver wire used.      (2)

Answer 1

(i) Since the circle is divided into 10 equal sectors, the total angle at the center is 360°.

Central Angle of each sector = `(360^@)/(10) = 36^@`

(ii) Find the radius of the circle 

`r = ("diameter")/(2) = 35/2 = 17.5 "mm"`

Use the arc length formula 

Arc length = `theta/(360^@) xx 2pir`

Substituting the values: 

Arc length = `36/360 xx 2 xx 3.14 xx 17.5`

= `1/10 xx 109.9`

= 10.99 mm

(iii) (a) Use the area of a sector formula

Sector Area = `theta/(360^@) xx pir^2`

Substituting the values: 

Sector Area = `(36)/(360) xx 3.14 xx (17.5)^2`

= `1/10 xx 3.14 xx 306.25`

= 96.11 mm²

OR

(iii) (b) Find the circumference of the circle 

Circumference = 2πr = 2 × 3.14 × 17.5 = 109.9 mm 

Since 5 diameters are drawn, each equal to the diameter of the circle:

Total diameter length = 5 × 35 = 175 mm

Total wire used = Circumference + Diameter length

= 109.9 + 175

= 284.9 mm