Question

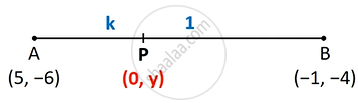
Find the ratio in which the y-axis divides the line segment joining the points (5, −6) and (−1, −4). Also, find the point of intersection.

Answer 1

Let the points be A(5, −6) and B(−1, −4)

Let point P the required point

Since point P is on y-axis

∴ its x coordinate is 0.

So, it is of the from P(0, y)

Now, we have to find ratio 

Let ratio be k : 1

Hence, 

m₁ = k, m₂ = 1

x₁ = 5, y₁ = −6

x₂ = -1, y₂ = −4

And 

x = 0, y = y

Finding x coordinate using section formula 

x = `(m_1  x_2 + m_2  x_1)/(m_1 + m_2)`

0 = `(k xx - 1 + 1 xx 5)/(k + 1)`

0 = `(-k + 5)/(k + 1)`

0(k + 1) = (−k + 5)

0 = −k + 5

k = 5

Hence, k = 5

Now, we need to find y also

y = `(m_1  y_2 + m_2  y_1)/(m_1 + m_2)`

= `(kxx-4+1xx-6)/(k+1)`

= `(5xx-4+1xx-6)/(5+1)`

= `(-20-6)/6`

= `(-26)/6`

= `(-13)/3`

Hence the coordinate of point is P(0, y) = P `(0, (-13)/3)`