Advertisements
Advertisements
Questions
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In ΔABC, if AD⊥BC and AD2 = BD × DC, then prove that ∠BAC = 90°.
Solution

Given: AD2 = BD × DC
`(AD)/(DC) = (BD)/(AD)`
∠ADB = ∠ADC = 90°
∴ ∆DBA ~ ∆DAC ...(SAS similarity)
So, these two triangles will be equiangular.
∴ ∠1 = ∠C and ∠2 = ∠B
∠1 + ∠2 = ∠B + ∠C
∠A = ∠B + ∠C ...(i)
By angle sum property,
∠A + ∠B + ∠C = 180°
∠A + ∠A = 180° ...[From (i) we get]
2∠A = 180°
∠A = ∠BAC = 90°
RELATED QUESTIONS
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
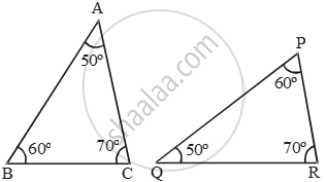
figure (i)
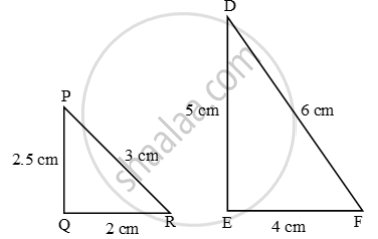
figure 2
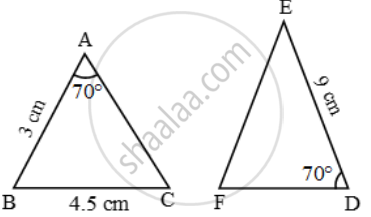
figure 3

figure 4
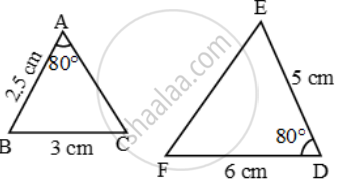
figure 5
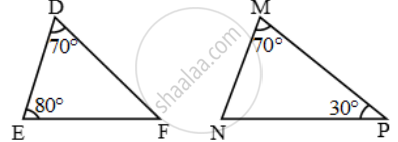
figure 6

figure 7
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
State, true or false:
Two similar polygons are necessarily congruent.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`

The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Which of the following is not a test of similarity?
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
