Advertisements
Advertisements
Question
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
Solution
Given, QR is parallel to AB.
Using Basic proportionality theorem,
`=> (PQ)/(PA) = (PR)/(PB)` ...(1)
Also, DR is parallel to QB.
Using Basic proportionality theorem,
`=> (PD)/(PQ) = (PR)/(PB)` ...(2)
From (1) and (2), we get,
`(PQ)/(PA) = (PD)/(PQ)`
PQ2 = PD × PA
APPEARS IN
RELATED QUESTIONS
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
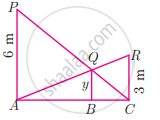
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
