Advertisements
Advertisements
Question
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Solution
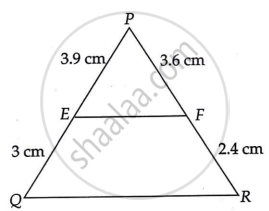
Given that PE = 3.9 cm,
EQ = 3 cm,
PF = 3.6 cm,
FR = 2.4 cm
`("PE")/("EQ")=(3.9)/3`
`39/30 = 13/10`
`("PF")/("FR") = 3.6/2.4 `
`13/10 != 3.6/2.4 `
Hence, `("PE")/("EQ") != ("PF")/("FR")`
Therefore, EF is not parallel to QR.
APPEARS IN
RELATED QUESTIONS
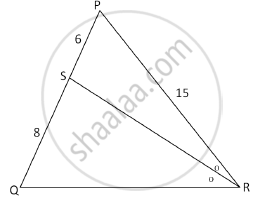
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
See the given figure. DE || BC. Find EC.

Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC

State, true or false:
Two congruent polygons are necessarily similar.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.
prove that
`("AM")/("PN")=("AX")/("PY")`
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.

Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

State the SSS-similarity criterion for similarity of triangles
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
Are the triangles in the given figure similar? If yes, by which test?

Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]

In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :
- `(CP)/(PA)`
- PQ
- If AP = x, then the value of AC in terms of x.

A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
A model of a ship is made to a scale of 1:500. Find: The length of the ship, if length of the model is 1.2.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

If figure OPRQ is a square and ∠MLN = 90°. Prove that QR2 = MQ × RN

If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
From the figure, prove that ∆SUN ~ ∆RAY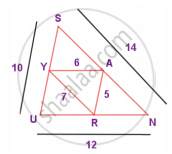
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
