Advertisements
Advertisements
प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
उत्तर
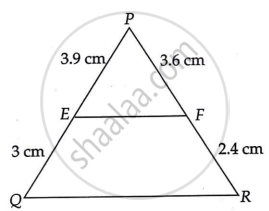
Given that PE = 3.9 cm,
EQ = 3 cm,
PF = 3.6 cm,
FR = 2.4 cm
`("PE")/("EQ")=(3.9)/3`
`39/30 = 13/10`
`("PF")/("FR") = 3.6/2.4 `
`13/10 != 3.6/2.4 `
Hence, `("PE")/("EQ") != ("PF")/("FR")`
Therefore, EF is not parallel to QR.
APPEARS IN
संबंधित प्रश्न
In figure, find ∠L

In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
See the given figure. DE || BC. Find EC.

See the given figure. DE || BC. Find AD.

E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
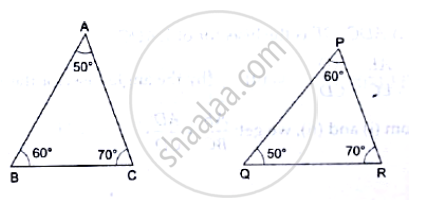
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
An aeroplane is 30m long and its model is l5 cm long. If the total outer surface area of the model is 150 cm2 , find the cost of painting the outer surface of the aeroplane at Rs. 120 per m2, if 5O m2 is left out for windows.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : A' B', if AB = 4 cm.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m3, find the volume of the tank on the top of the model.
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
Through the vertex S of a parallelogram PQRS, a line is drawn to intersect the sides Qp and QR produced at M and N respectively. Prove that `"SP"/"PM" = "MQ"/"QN" = "MR"/"SR"`
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
In ΔABC, DE || BC such that AD =1.5 cm, DB = 3 cm and AE = 1 cm. Find AC.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
The dimensions of the model of a building are 1.2m x 75cm x 2m. If the scale factor is 1 : 20; find the actual dimensions of the building.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
Check whether the triangles are similar and find the value of x
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
In a square of side 10 cm, its diagonal = ______.
In ∠BAC = 90° and AD ⊥ BC. A then ______.

In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.
In the adjoining diagram the length of PR is ______.

