Advertisements
Advertisements
प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
उत्तर
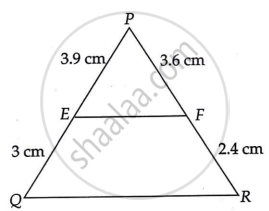
Given that PE = 3.9 cm,
EQ = 3 cm,
PF = 3.6 cm,
FR = 2.4 cm
`("PE")/("EQ")=(3.9)/3`
`39/30 = 13/10`
`("PF")/("FR") = 3.6/2.4 `
`13/10 != 3.6/2.4 `
Hence, `("PE")/("EQ") != ("PF")/("FR")`
Therefore, EF is not parallel to QR.
APPEARS IN
संबंधित प्रश्न
In figure, find ∠L

In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
In figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, find CA and AQ.
In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
The two similar triangles are equal in area. Prove that the triangles are congruent.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, ∠ABC = 90° and BD⊥AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

ΔABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ΔABC and ΔADC.
State the AA-similarity criterion
As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
In the given figure, seg XY || seg BC, then which of the following statements is true?

ABCD and PQRS are similar figures. AB= 12cm, BC=x cm, CD= 15 cm, AD= 10 cm, PQ= 8 cm, QR = 5 cm, RS = m cm and PS = n cm .Find the values of x, m and n.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
On a map drawn to a scale of 1 : 25000, a triangular plot of a land is marked as ABC with AB= 6cm, BC = 8cm and ∠ ABC = 90° . Calculate the actual length of AB in km and the actual area of the plot in km2 .
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,
Find
(i) AQ
(ii) PQ
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The number of KM represented by 2cm on the map.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The ground area in km2 that is represented by 2cm2 on the map.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
A model of a ship is made to a scale of 1:500. Find: The length of the ship, if length of the model is 1.2.
In a triangle ABC, AB = 4 cm, BC = 4.5 cm and CA = 5 cm. Construct ΔABC. Find the image A'B'C of the ΔABC obtained by enlarging it by a scale factor 2. Measure the sides of the image A'B'C' and show that AB:A'B' = AC:B'C' = CA:C'A'
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
From the figure, prove that ∆SUN ~ ∆RAY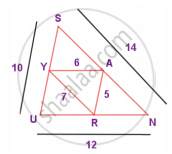
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

Are triangles in figure similar? If yes, then write the test of similarity.
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

If ΔABC ~ ΔLMN and ∠B = 40°, then ∠M = ? Give reason.
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

