Question

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Answer 1

i. In ΔACB and ΔFCE, we have

∠ACB = ∠FCE  ...(Vertically opposite angles)

∠CBA = ∠CEF  ...(Alternate angles)

∴ ΔACB ∼ ΔFCE  ...(AA axiom of similarity)

Thus their corresponding sides are proportional.

∴ `(AB)/(BC) = (EF)/(EC)`

`\implies (7.5  cm)/(x  cm) = (4.5  cm)/(3  cm)`

`\implies x = ((7.5 xx 3)/4.5) cm`

= `225/45 cm`

= 5 cm

ii. In ΔEBF and ΔCBD, we have

∠B = ∠B  ...(Common angle)

∠EFB = ∠CDB  ...(Corresponding angles)

∠BEF = ∠BCD

∴ ΔEBF ∼ ΔCBD  ...(AA axiom of similarity)

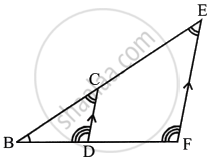
Thus, `(EB)/(CB) = (EF)/(CD)`

`\implies (EC + CB)/(CB) = (4.5  cm)/(y  cm)`

`\implies (3 + x)/x = 4.5/y`

`\implies ((3 + 5)  cm)/(5  cm) = 4.5/y`

`\implies y = (4.5 xx 5)/8`

= `45/16 cm`

= `2 13/16 cm`